빅오(Big-O) 표기법과 시간복잡도

 

1. 빅오 표기법이란?

 

알고리즘이 해당 차수이거나 그보다 낮은 차수의 시간복잡도 및 공간복잡도를 가진다는 의미이다.

프로그램이 돌아가는 동안, 정확한 단계(step) 의  수를 결정하는 작업은 매우 어렵고 복잡하기 때문이다.

예를 들면 3n+5는 3n과 근사한 것으로 판단한다는 뜻이다.

 

빅오 표기법은 f(n)∈O(g(n))과 같이 표기된다.

O(n), O(n^2) 등과 같이 표기 되며 O(n+10)=O(n)으로 간주한다고 생각하면된다.

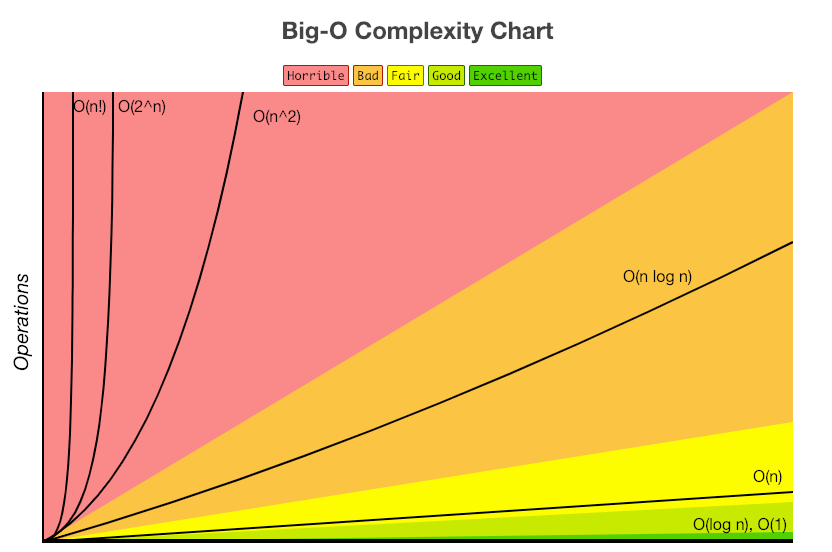
위 그래프와 같이 빅오 표기법은 성능(수행시간 및 횟수)은 다음과 같다.

O(1) < O(log n) < O(n) < O(n * log n) < O(n²) < O(n³) < O(2^n) < O(n!)

 

O(n^2)이상의 성능을 가지는 알고리즘은 가용가치가 없다고 판단하면 된다.

 

 

2. 시간복잡도와 공간복잡도

시간복잡도

컴퓨터 프로그램의 입력값과 연산 수행 시간의 상관관계를 나타내는 척도이다.

 

1) O(n) 복잡도

/*곱셉연산 하나만 사용하므로 O(n)*/

funtion multiple(num){
	return n*n
}


/*배열에 push, pop등 하나의 요소에 접근하므로 O(n) */

function addElement(arr, val){
	return arr.push(val)
}

 

2) O(log n) 복잡도

int a = 0, i = N;
while (i > 0) {
    a += i;
    i /= 2;
}

 

3) O(n^2)

int a = 0;
for (i = 0; i < N; i++) {
    for (j = N; j > i; j--) {
        a = a + i + j;
    }
}